The electrons form spatial constructs with other electrons. Twelve electrons will configure into a spatial arrangement of a dodecahedron. It is the building stone of protons and neutrons.

On each face of such a dodecahedron is an electron active.
At first sight, this is counterintuitive. Regular science assumes that electrons always mutual repel due to the similar isotropic electric charge.
Therefore we need to have a better understanding of the oscillation behavior of naked electrons.
The animation of an electron is:
The electron oscillates in chirality at a frequency of 10¹⁴ Hz. As explained, this oscillation is due to the small difference in frequency of the gamma photon relative to the gamma neutrino in the electron. At the change-over of chirality, the electric manifestation of the photon makes a change-over to opposite asymmetry.
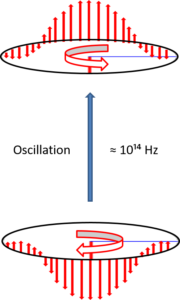
As a naked electron, that oscillation is from electron into a positron. When more electrons are present, then these electrons can mutually attract each other provided that they rotate into a position of attraction. Such a rotation is alike as shown with this simple set up of magnets:

Therefore, the electrons can rotate towards each other at the frequency of maximum approx. 10¹⁴ Hz.
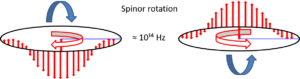
It is the second part of the spinor action.
In case of a proton present, this spinor rotation of the electron would be at every oscillation, but there are no protons yet. When protons are absent, the electrons oscillate in the frequency of 10¹⁴ Hz and occasionally might rotate if potential attracting is possible. Each naked electron shows this behavior and therefore will neither attract or repel relative to each other.
In the very early stage of development of the universe, these electrons were formed in abundance amid an overwhelming mix of other electrons, gamma photons, and neutrinos as well. It is difficult to visualize how new constructs could emerge out of such a seemingly wild and complex mixture of particles.
Nevertheless, this is possible. Electrons may collide at an angle. If so, that adds the activity of the Lorentz force to the Coulomb force,

The asymmetrical electric manifestation meets de magnetic manifestation of another electron, and consequently, they become mutually subjected to the Lorentz force. This Lorentz force introduces a spatial and random movement of such a couple of electrons.
The Dutch Paradigm postulates that out of the mix of particles, ad random spatial configurations of electrons emerge in a dodecahedrons arrangement.
In an illustration:
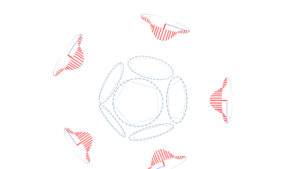
12 electrons might accidentally collide in a spatial arrangement of a dodecahedron, with an electron on each face. Once such an arrangement is there, each electron will exert Lorentz forces with neighboring electrons. The vectors of these forces are all pointing inwards to the opposite electron.
In such an arrangement, the 12 electrons are locked in position with very strong Lorentz forces. This arrangement, therefore:
- is extremely stable
- propagates at speed zero compared to the speed of light
- is electrically neutral
- the resulting spin is neutral
- free spinor rotation per electron is not possible anymore
Moreover, once such a dodecahedron arrangement forms, it excludes itself from the mix due to the difference in speed and electric neutrality. The total mix of particles at relativistic speed reduce gradually with each dodecahedron arrangement formed. The dodecahedron is the only arrangement of the Plato “solids” able to configure a stable construct of electrons.
Even so, we still have entities without a spatial extension in a construct. It is the interference pattern of their electromagnetic manifestations that we can imagine as a spatial form of a dodecahedron in exhibiting the combined electromagnetic manifestations. There is no substance involved, while there is a mass manifestation.
Constructs of 12 electrons in a dodecahedron arrangement encounter other particles and also similar arrangements of 12 electrons in a dodecahedron arrangement. It will form twin dodecahedrons as the arrangements for the constructs neutron and proton.
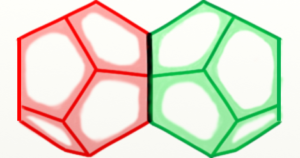
Before discussing twin dodecahedrons, we need to understand in more detail the behavioral characteristics of such a dodecahedron arrangement of electrons.
